2025. január–február, XXXII. évfolyam, 5–6. szám, ISSN 2729-9066

 
Juhász Valéria

A számolási képesség előfeltételei, annak nyelvi fejlettséghez kapcsolódó kérdései
A mennyiségreprezentációk és a kezdeti számlálás, számolás jelenléte állatoknál, a számrendszerrel nem rendelkező törzseknél

Bevezetés

A következő, háromrészes cikksorozatban a számolási képesség fejlődésével foglalkozom, annak alapjaival, különös tekintettel azzal, hogy a nyelvi kód mennyire nélkülözhetetlen szerepet játszik a számolással kapcsolatos dolgok elsajátításában. A számlálási, ¹ számolási, ² képesség fejlődése, a mennyiség­reprezentációk kialakulása bizonyos szinttől kezdve nem működik a nyelvi kód ismerete nélkül. Az első részben arról lesz szó, hogy miféle mennyiségismerettel rendelkeznek az állatok, miért érdekes ez az ember számolási képességének megismerésével kapcsolatban, továbbá hogy a számrendszerrel nem rendelkező törzsekkel folytatott kísérletek mit igazoltak a számolás alapjaival, a mennyiségreprezentációk jelenlétével kapcsolatban. A számolási képesség további összefüggéseinek megértéséhez részletezem – a terjedelmi korlátok megtartása mellett – Dehaene hármaskód-modelljét.

A sorozat dedikált célja, hogy a matematikához (algebrához/ aritmetikához és a geometriához) kötődő képességeket a nyelvi képességek fejlődésének a vetületében mutassa be, azaz jelen írás nem tartozik szorosan a matematikatanítás módszertanához, hanem a nyelv elengedhetetlen voltát, a fogalmak kialakítását és alapvető szükségszerűségét emeli a fókuszba. Az életkor szempontjából a tanulmány az iskola előtti, illetve az iskolába lépő korosztályra fókuszál, mert a matematikai műveletekhez tartozó egyes kifejezések ismerete ebben a korai életkorban hozzátartozik az iskolaérettséghez.

A második részben foglalkozom a számolási képesség fejlődésével, a számolási képességet mérő tesztekkel, illetve röviden az óvodáskorúak számolási képességének a fejlesztésével, a harmadik részben pedig a matematikai feladatok és a szövegértés összefüggésével.

Kiindulópontként idézzük Krajcsi (2014) tanulmányát, amelyben alapvetésként fogalmazza meg, hogy bármiféle, számolással kapcsolatos tevékenység megkezdéséhez legalább két alapvető dologra van szükség: az egyik egy mennyiségrendszer észlelése valamilyen formában, a másik a vizuális tárgyfelismerő rendszer, amely legfeljebb 4 tárgyat tud követni. Ez minden „számolási” feladat előfeltétele.

Állatokkal végzett számolási kísérletek

Gyakori kérdésként lehet hallani ezen a területen nem jártas, de érdeklődő emberektől, hogy az állatok tudnak-e számolni. Vajon mi ennek a jelentősége az emberek számolási képességében? Az állatok viselkedéséből, illetve a velük folytatott kutatásokból az emberre is vonatkoztatva számos dolgot megérthetünk. Ehhez még az is hozzájárul, hogy az állatok kommunikálnak ugyan, de nem beszélnek. Akkor tudnak vajon számolni? Hauser (2002) Vad elmék című könyvében ír az állatok számolási képességéről. Az állatoknak több szempontból is rendelkezniük kell valamiféle mennyiségismerettel, ez összefüggésben van:

1. a táplálékhely-találó tevékenységgel és az ezzel arányos, optimális energiabefektetéssel, itt például igen közismert a méhek kommunikációja a táplálékhely-keresésre vonatkozóan;
2. az egymással folytatott vetélkedéssel, például a palackorrú delfinek csoportosulni is tudnak más csoportokkal, hogy legyőzzék a harmadik csoportot;
3. az ellenfél összetételének felmérése kapcsolódik még a párkereséshez is: például amikor a hím oroszlán a meghódítani kívánt oroszlánfalka bömbölésének hangösszetétel-elemzésével méri fel, milyen esélye van a másik csapat megtámadására, hogy ő lehessen a nőstény oroszlánok új „kakasa”.

Egyes elképzelések szerint a vizsgált állatok az egy-több-kevesebb-sok mennyiség-megkülönböztető képességgel rendelkeznek.

A cirkuszban bemutatott állatok számolási képességeiről kiderült, hogy az emberek egyéb metakommunikatív jeleiből (például Hans, az okos ló esete) ³ tudják azonosítani a számokat, „tudnak” számolni, összeadni stb. (Hauser, 2002). Hauser számos kísérletről számol be olyan állatokkal (patkányokkal, galambokkal) kapcsolatban, amelyeket számolni tanítottak. Köztük az Irene Pepperberg Alex nevű, híres afrikai szürkepapagájáról is ír, ⁴ aki több évig tanult beszélni, és ki tudott fejezni olyan komplex fogalmakat, mint a néhány, az egy se, a semmi, és száznál több szót, főleg igéket és főneveket, különféle rövidebb kifejezéseket tudott mondani, de igazi nyelvi rendszere nem fejlődött ki. Alex értette, hogy mi az, ami színben, formában, anyagban, nagyságban ugyanolyan; mi az, ami különböző. Színeket, formákat, anyagokat tudott megnevezni, és meg tudta mondani hatig ⁵ a dolgokról, hogy az hány darab, vagy akár számkép alapján is helyesen döntött arról, hogy melyik a több. Alex különféle tárgyfajták csoportosításával és színkombinációk alkalmazásával is tudott szelektálni és összeadni. Úgy tűnik, tudott gondolkodni, következtetéseket levonni. ⁶ Vagyis ezek alapján belátható, hogy a papagájok is számos olyan veleszületett megkülönböztető képességgel rendelkeznek, amelyekre kis mértékben építhető nyelvi és számolási rendszer. Mindez azt jelenti, tisztában vannak a nyelv mint absztrakt és önkényes szimbólum és a tárgy egymáshoz rendelt viszonyával, a tulajdonságdifferenciákkal, illetve a kardinalitással (ami a megszámolt dolgok utolsó száma, a tárgyak összege) (Hauser, 2002, 87). Lehet, hogy ezeknek az állatoknak van valamiféle kezdetleges számolási képességük, valamilyen számkategória-ismeretük, de számfogalommal nem rendelkeznek.

Egy másik, számolási kísérletbe bevont állat volt Matsuzawá Ai nevű csimpánza. Ai, ahogy Hauser írja, 10-ig ismerte a számsort; egy 1 és 10 közötti számsort nagyság szerint tudott rendezni ⁷  – függetlenül a számok közti különbség mértékétől (például 5-1-4-et rendezte 1-4-5 sorrendben) –, vagyis értette a számok közti viszonyokat, ami azt jelentette, hogy Ai tanítás hatására el tudta sajátítani a számfogalom bizonyos aspektusait. Mind Alexszel és Aival, mind további bunder- és selyemmajmokkal folytatott kutatásokban arra jutottak, hogy a tanított majmok jóval többéves munkával sajátították el az absztrakt számértéshez kapcsolódó, a megtanult elemekhez képest eggyel nagyobb számok ismeretét, a számok összeadását, kivonását, mint a gyerekek. Ám mindezek is csak kis számokkal működtek (többnyire körülbelül háromig), ami azt jelenti, hogy más módon képezik le a számokat, mint az ember. ⁸ Az állatok mögöttes mentális műveleteiről különféle elképzelések vannak, de biztos, hogy az emberre jellemző számolási képességgel (például a számfogalmi hiányosságaik miatt) nem bírnak, illetve csak nagyon kis számokkal tudnak valamiféle számoláshoz kapcsolódó műveletet elvégezni, ám rendelkeznek a fentebb felsorolt, a létfenntartáshoz szükséges relatív mennyiségfelismerő és -összehasonlító képességgel. Azt, hogy a gyermekek általánosságban már az első három év után – viszonylag gyorsan – magasabb szintre fejleszthető számolási, matematikai képességgel rendelkeznek, a nyelv elsajátításának tulajdonítják, ami alkalmas a számlista és az ahhoz kötődő számrendszer konceptuális ⁹ megértésére (Hauser, 2002, 88–93).

Számokat nem vagy csak kismértékben használó törzsek aritmetikai képességei

Vizsgálták olyan törzsek (például mundurukuk, pirahák) számolási képességét is, akiknél nincsenek számok, vagy csak 1 és 5 közti számokat, illetve csak az egy, a kettő és a sok számneveket használták – azokat sem megfelelően, vagyis az általunk ismert/ használt módon. Számolásuk így nem tud pontos lenni, viszont az analóg mennyiségreprezentációban (ami a mentális számegyeneshez kötődik és a becslésben segít) jól teljesítenek. Ez hasonlít az állatok „számolási” rendszeréhez (Krajcsi, 2014).

A számolás előfeltételei, összetevői

Dehaene (2003) hármaskód-modellje szerint számoláskor három különböző, de egymással összekapcsolt reprezentációs rendszert használunk: analóg mennyiségreprezentációt, a szám nevét vagy „vizuális arab számformátumot”.

Az analóg mennyiségreprezentáció, vagy másként a mentális számegyenes, közelítő számossági rendszer a számmegértés alapja. Ez a balról jobbra, felülről lefelé történő írásrendszereknél egy olyan téri jellegű információ, amely szintén balról jobbra halad egy tengelyen a kisebbtől a nagyobb számok felé. Ez segít a becslésekben, összehasonlításokkor, a közelítő összeadásokban ¹⁰ és egyesek szerint a szubitizációban (a négy és az az alatti számosság felismerésében). A szubitizáció azt jelenti, hogy számolás nélkül, rápillantással, bármilyen elrendezésben meg tudjuk mondani, hányat látunk. Négy fölötti számoláskor is úgy tűnik, hogy rápillantással mondjuk meg, hogy például nyolcat látunk, de ez inkább csak a kanonikus elrendezéseknél sikeres. A kanonikus elrendezés azt jelenti, ahogy a dobókockán, a dominón megjelenítjük a szokásos módon a tárgyakat, vagy ahogy az ujjainkkal mutatjuk a számokat. A tárgyak elrendezésének tehát jelentős szerepe van számoláskor (Juhász és Radics, 2017, 2019). Vagyis a szokásos, kanonikus elrendezésben könnyebb felismerni a számosságot, mint az attól eltérő elrendezésben. (Diszkalkuliaterápiában ettől eltérően a pöttyöket minél távolabb helyezik el a négyzetben, például Farkasné Gönczi és Szabó, 2018).

 
1.ábra: Az öt kanonikus megjelenítése dobókockán, dominón és az ujjakon
Az ábrát Heraszika Viktória készítette a Beszédfejlődés segítése… című könyvemhez Forrás: Juhász, 2023, 103
 

A nem kanonikus elrendezésekben inkább valamiféle csoportosításokban adjuk össze, hogy itt négy van, ott kettő, ott egy, tehát ez hét. De mindez olyan gyorsan történik, hogy szinte rápillantásszerűnek érezzük, és nem négy alatti számokkal történő csoportosításos összeadásnak.

 
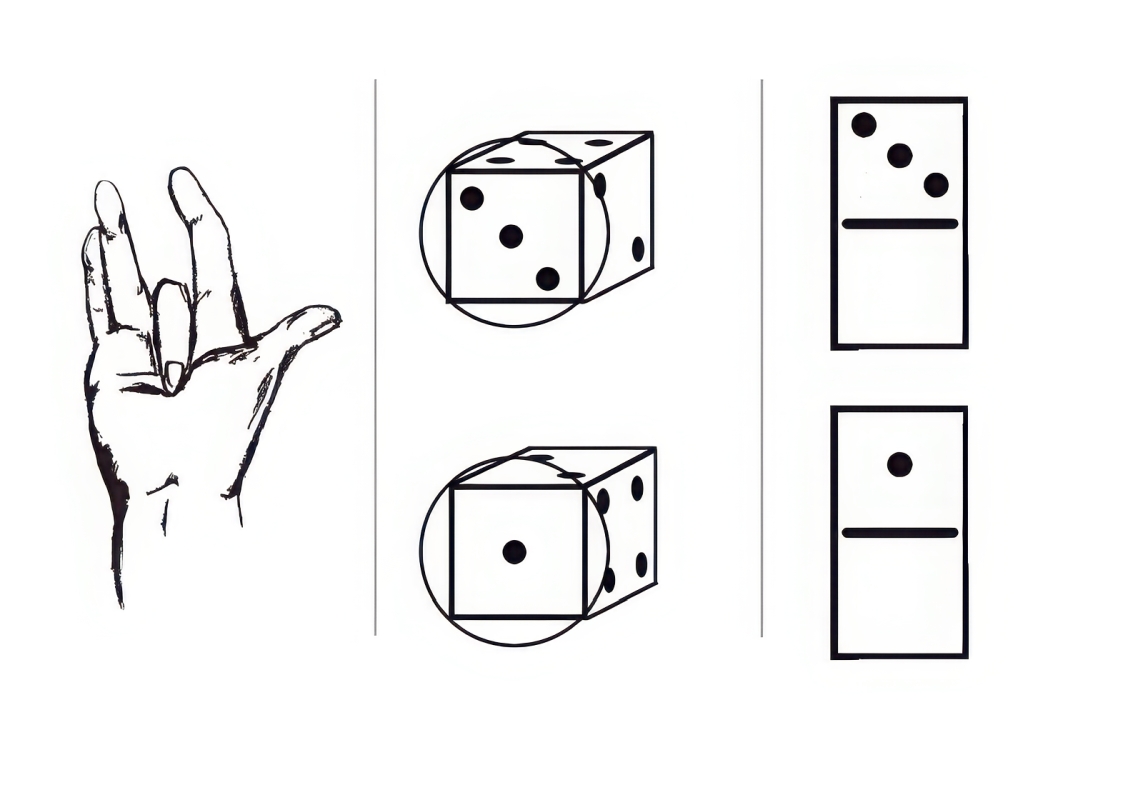
2.ábra: A négy nem kanonikus elrendezésben dobókockán és ujjakon
Az ábrát Heraszika Viktória készítette
 

Nézzük meg, hogy a kisgyermek, ha egymás alá rajzolunk három pöttyöt, egy kicsit távolabb tőlük még egyet: így is felismeri-e a négyet. Vagy ha két dobókockát teszek egymás mellé, az egyiken egy pöttyöt lát, a másikon hármat, sikerül-e átlátnia, hogy az négy pötty. Ennek gyakorlására számos társasjátékot lehet kapni, bármilyen tárggyal lehet gyakorolni, gombokkal, pálcikákkal, kaviccsal, termésekkel, és ne feledjük, a kéz mindig kéznél van!

Ez az analóg mennyiségreprezentációs rendszer nem tudja pontosan tárolni az információt, csak körülbelül határozza meg a mennyiséget, úgymond „zajosan”, átfedésekben más számokkal. Minél nagyobb a szám, annál pontatlanabb a tárolás, annál nagyobb átfedése van más számokkal. Minél nagyobb két jel, és minél kisebb köztük a relatív különbség, annál nehezebb megkülönböztetni őket. Ezt nevezzük a numerikus távolsági hatásnak. Például a 3 és 5 közti relatív különbség (0,66) kisebb, mint a 153 és 155 közti (0,1). ¹¹ Egyedekre jellemző, hogy mennyire pontosak a becslésekben, de az életkor előrehaladtával ez a képesség fejlődik. Egyes elképzelések szerint ennek a rendszernek a fejlettsége összefüggést mutat az iskolai matematikai teljesítménnyel, ezért ennek a fejlesztése a matematikai eredményekben is teljesítményjavulást eredményezhet (lásd még tovább: Krajcsi, 2010, 2014, 2022). ¹²

A szám neve, az „auditoros verbális szókeret” vagy másként egy verbális rendszert jelent, ami a számokat hangsorokként, betűsorokként tárolja. Ez képes a számokat pontosan/ diszkréten tárolni (ez az egy az egyhez való megfelelés), de ez a rendszer önállóan nem érti, hogy mit tárol, hiszen ezek önmagukban csak hangsorozatok. Ez tárolja a szorzótáblát is, és ez köti össze a különféle reprezentációs rendszereket. ¹³

A „vizuális arab számformátum” képes a számokat pontosan tárolni. Feltételezhetően a párosságot is ez segíti megállapítani: hiába halljuk a hangsort, átfordítjuk arab számmá, hogy a párosságot el tudjuk dönteni.

Egyes kutatások szerint a matematikai teljesítmény csak a szimbolikus szám-összehasonlítással mért teljesítménnyel függ össze, a nem szimbolikussal már nem annyira (De Smedt, Noël, Gilmore és Ansari, 2013 munkáját idézi: Krajcsi, 2022). Fejlődési diszkalkuliásokat vizsgálva azt találták, hogy a fiatalabb gyerekeknél csak a szimbolikus, azaz a számokkal kapcsolatos műveleteknél találtak deficitet, és a nem szimbolikus feladatok sérülése csak később, 9–10 éves kor körül jelent meg, amit a mentálisszámegyenes-elmélet nem tud magyarázni, illetve éppen fordítva magyarázna (Noël és Rousselle, 2011 munkáját hivatkozza Krajcsi, 2022).

A három rendszer kapcsolatban áll egymással, az idegrendszerben más-más területek működése felelős a három rendszerért (Krajcsi, 2022). McCloskey (1992) folyamatorientált modellje szerint a számolás kialakulásához el kell különíteni magukat a mennyiség megértésére és produkciójára vonatkozó tényeket (a számok különféle formáját, például a számformátum vagy a hangsor bemenete és kimenete), illetve a velük végzett műveleti folyamatokat: az összeadást, szorzást stb. A procedurális folyamatokhoz tartozhat a számok (verbális és számkép) átfordításának képessége is (McCloskey, 1992; Barrouillet, Camos, Perruchet és Seron, 2004 munkáit idézi Krajcsi, 2014).

A következő részben az ember számolási képességének fejlődésével foglalkozom, továbbá az ezt mérő teszteket mutatom be, de ezek közül is csak azokat, amelyeket iskolába lépésig használnak.

A tanulmány bírálati folyamaton ment keresztül.

Felhasznált irodalom

Barrouillet, Pierre–Camos, Valérie–Perruchet, Pierre–Seron Xavier (2004): ADAPT: a developmental, asemantic, and procedural model for transcoding from verbal to arabic numerals. In: Psychological Review, 111. évf., 1. sz., 368–394. ISSN: 1939-1471. doi: 10.1037/0033-295X.111.2.368.

De Smedt, Bert–Noël, Marie-Pascale–Gilmore, Camilla–Ansari, Daniel (2013): How do symbolic and non-symbolic numerical magnitude processing skills relate to individual differences in children’s mathematical skills? A review of evidence from brain and behavior. In: Trends in Neuroscience and Education, 2. évf., 2. sz., 48–55. ISSN: 22119493. doi: 10.1016/j.tine.2013.06.001.

Dehaene, Stanislas (2003): A számérzék. Miként alkotja meg az elme a matematikát? Budapest, Osiris Kiadó.

Farkasné Gönczi Rita–Szabó Otília (2018): Számoljunk együtt – a számolási zavarok leküzdéséért. In: Gereben Ferencné – Cserti-Szauer Csilla (szerk.): Gyógypedagógia – dialógusban. Budapest, MAGYE, ELTE Bárczi Gusztáv Gyógypedagógiai Kar, 45–52, ISBN: 978-963-7155-80-2,

Hauser, Marc D. (2002): Vad elmék. Mit gondolnak az állatok? Budapest, Vince Kiadó.

Juhász Valéria (2023): A beszédfejlődés segítése, a nyelvi tudatosság fejlesztése a sikeres olvasásért és tanulásért. Papír-ceruza-dobókocka játékgyűjteménnyel óvodásoknak és kisiskolásoknak. Szeged, JGYF Kiadó, ISBN: 978-615-5946-87-5.

Juhász Valéria–Radics Márta (2017): Ujjtudatosság a számolásfejlesztésben óvodás-, illetve kisiskolás korban: Ujjpercepciós, ujjtudatosságot fejlesztő gyakorlatok. In: Új Pedagógiai Szemle, 67. évf. 11–12. sz., 50–72., ISSN 1788-2400.

Juhász Valéria–Radics Márta (2019): Ujjtudatosság a számolásfejlesztésben óvodás-, illetve kisiskoláskorban. Ujjpercepciós, ujjtudatosságot fejlesztő gyakorlatok. In: Juhász Valéria–Kálló Veronika–Radics Márta (szerk.): Anyanyelvi nevelés, írás-olvasás előkészítés óvodás- és kisiskoláskorban. Szeged, Szegedi Egyetemi Kiadó, Juhász Gyula Felsőoktatási Kiadó. 183–206. ISBN: 978-615-5946-12-7.

Kabai Péter (2011): A madarak énektanulásáról. In: Magyar Tudomány, 172. évf., 8. sz, 920–928. ISSN: 1588-1245 http://epa.niif.hu/00600/00691/00092/pdf/mtud_2011_08_0920-0928.pdf. (Letöltés ideje: 2024. 10 04.)

Krajcsi Attila (2010): A numerikus képességek zavarai és diagnózisuk. In: Gyógypedagógiai Szemle, 38. évf., 2. sz., 93–113.

https://epa.oszk.hu/03000/03047/00049/pdf/EPA03047_gyosze_2010_2_093-113.pdf. (letöltés ideje: 2024. 10 04.)

Krajcsi Attila (2014): Nyelvi reprezentáció a numerikus feladatokban. In: Lukács Ágnes – Pléh Csaba (szerk.): Pszicholingvisztika 2. Budapest, Akadémiai Kiadó, ISBN: 978-963-05-9501-8 919–950.

Krajcsi Attila (2022): A számok megértése. In: Pléh Csaba (szerk.): Pszichológia. Budapest, Akadémiai Kiadó, ISBN: 978–963–454–639–9.

https://mersz.hu/dokumentum/m880pk__294/#m880pk_292 (letöltés ideje: 2024. augusztus 13.) DOI: 10.1556/9789634546399.10.

McCloskey, Michael (1992): Cognitive mechanisms in numerical processing: Evidence from acquired dyscalculia. In: Cognition, 44. évf., 1–2. sz., 107–157. ISSN:1873-7838, doi: 10.1016/0010-0277(92)90052-J. https://linkinghub.elsevier.com/retrieve/pii/001002779290052J (letöltés ideje: 2024. 08. 10.)

Noël, Marie-Pascale–Rousselle, Laurence (2011): Developmental Changes in the Profiles of Dyscalculia: An Explanation Based on a Double Exact-and-Approximate Number Representation Model. In: Frontiers in Human Neuroscience, 5. évf., 165. sz., ISSN: 1662-5161, doi: 10.3389/fnhum.2011.00165.

http://journal.frontiersin.org/article/10.3389/fnhum.2011.00165/abstract (letöltés ideje: 2024. 08. 24.).